Below you will find a list of activities that may be suitable for this age group. Please remember, however, that a child’s ability to engage with any activity will depend more on their prior experience and understanding than on their chronological age. Please, therefore, also browse the activities for adjacent age groups.
Fractions and Percentages Of and Off
In this extended exploration we use a metre stick or counting stick as a representation of the whole or 100%, and explore mental strategies for finding different fractions and percentages of an...
What links can we find between fractions and percentages?
This activity was specifically designed to support the following learning intention: How can we use a metre stick, a hundred square and the factor rainbow for 100 to explore the link between...
How much can we learn about multiples and factors?
This activity is aimed at children who have a basic experience of multiples and factors and whose learning needs to be consolidated or deepened. It is in three parts. Part 1 explores multiples, Part...
Populations
This exploration introduces pupils to the Worldometer population table and then gives them various challenges to consolidate their skills in finding information in a table, reading large numbers...
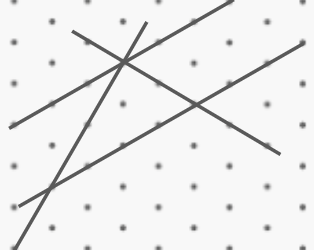
Lines, Angles and Shapes
This single resource allows for the consolidation and development of a wide range of mathematical skills and concepts, covering line, angle, shape, symmetry, area and proportionality. It can be...
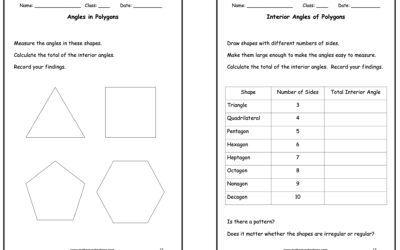
Angles in Polygons
Investigate the total interior and exterior angles of polygons (triangle, quadrilateral, pentagon, hexagon etc.) Explore patterns in the numbers and establish rules and experiment with formulas.
Constructing Shapes
Constructing shapes with compasses is always great fun because you get pretty patterns. But this investigation goes well beyond regular activities with pupils being given an open-ended challenge to...
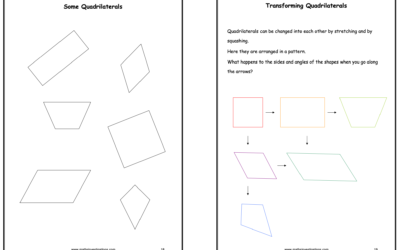
Properties of Quadrilaterals
Find out why a square is a special kind of rectangle but a rectangle is not a special kind of square!Explore the differences rhombuses and parallelograms, kites and trapeziums.Investigate questions...
Pythagoras Puzzle
Have fun making this simple puzzle which very beautifully illustrates Pythagoras’ Theorem that the sum of the squares on two sides of a right-angled triangle = the square on the third side. Make...
How Tall is that Building?
An outdoor team challenge to estimate the height of a building, either by counting bricks, using shadows or using similar triangles. Covers skills in estimating, measuring, minimising errors and...
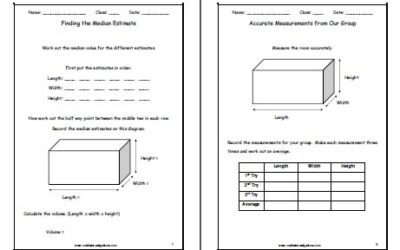
How Much Snow Would Fill the Classroom?
Estimate distances, work with volume of cuboids, convert metric volumes - cm3 - litre - m3, measure with metre sticks, minimise sources of error, average using the median, draw diagrams, round...
Equations Through Pictures
Straight line graphs are often not taught until somewhere in the middle secondary years. But they can actually be an excellent way of helping younger children to explore how equations work if you...
Election Results
Compare the results of a recent election with a previous one and present findings using a hand drawn pie chart. Covers the skills of expressing quantities as percentages and calculating pie chart...
The Algebra of Throwing
Children often ask what algebra is FOR. This investigation allows capable pupils at the top end of primary school to use simple algebraic skills to investigate an area of Maths that is normally...
Train Journey
Investigate how to use train timetables, calculate journey times, interpret maps, measure distances, use averages and work with scale. Create an information booklet about a forthcoming train...
Formulas for Sequences
Investigate the connection between number sequences and the rules that generate them. Begin by exploring two simple matchstick patterns and develop into investigating line graphs for formulas.
Not found what you want?
Search by Topic
